dla3d dla3d
I think it started earlier this year, when I witnessed the fractal-like dendrites of DLA in two places: fingers of a growth on a rock at the National Science Museum on the Mall in DC,
(also here and here, or just look at all of the pictures I took there), and lichen growth on a rock at Great Falls Nat'l Rec Area.
Then on Sunday thru Tuesday of this week, I had been paging through Barabasi and Stanley's "Fractal Concepts in Surface Growth" book, and I noticed the chapter on DLA. I wanted to create the shapes on my computer, but didn't think the basic algorithm was fast enough (they never are). One makes an image of DLA by releasing a particle a distance from a seed particle, and letting the released particle perform a random walk until it hits the seed particle, then freezing it and releasing another particle.
On Wednesday, while I should have been thinking about work, I thought of a way to speed that up. A random walker has an even chance of ending up on any point on the surface of a sphere, as long as the sphere is free of obstructions. This means that I can skip thousands of steps by simply determining how far the current particle is from the nearest frozen particle, and then moving the current particle that distance in a random direction. Hopefully, it'll move close enough to the frozen structure to intersect one of the frozen particles and become frozen itself. If the particle chooses to move away from the frozen structure 5-10 times in a row, just kill it and start a new one. Because the particles occupy a point in free space, and are not confined to grid motion, the simulation is called off-lattice DLA.
So, on Wednesday night, I took my 3D particle system program and stripped it down to the inputs, outputs, and octree spatial subdivision code. Then, I built up a 3D DLA code. It was working before I went to bed.
The next day I fixed some bugs that were slowing it down and producing too much overlap, and most of the day yesterday was spent tending some runs and rendering some images. Keep in mind that the photos above are 2D DLA, and the program I wrote only does 3D. I suppose I could write it to do things in 2D, but I'm not that motivated.
Rendering of 8000 spheres in 3D DLA
X-ray of 95000 particles in 3D DLA
Rendering the 9900 segments of the connectivity branches of a 3D DLA
Continuing with the story, last night, as El read an ebook, I curled up with Gleick's Chaos and read about how simple imbalances of three-equation dynamical systems give rise to a near-infinity of shapes. Case in point: the balance of forces in a growing snowflake teeters between surface tension of liquid water and diffusion of the heat released when water freezes. These forces swap importance as the temperature and humidity vary, even very slightly. Since a single snowflake is so small, its entirety encounters almost the same external influences the whole way down to the ground, resulting in nearly symmetric snowflakes. Now, since turbulence makes every snowflake's path through space and its influencing fields of temperature and humidity different...we have a saying for this.
After reading Gleick for two hours, I looked outside and Gaithersburg had received its first snowfall of the winter.
230,000 segments of the largest 3D DLA that I have run
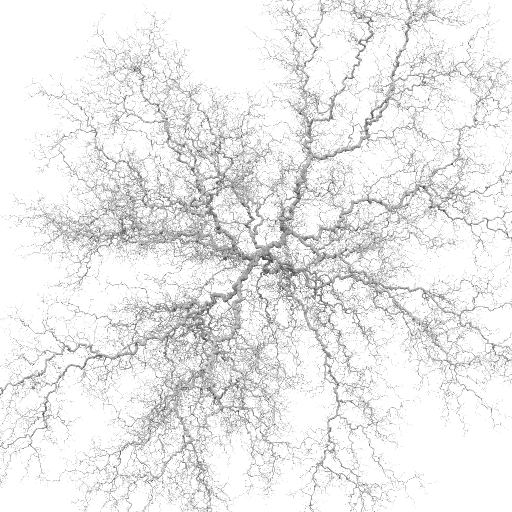Stickiness = 1.0
Stickiness = 0.1
Stickiness = 0.01
The program took about 20 minutes per 1000 particles for the 1.0 case, at the 100,000-particle level, on a P4-1.6 machine. The 0.1 case took twice as long as the 1.0 case, and the 0.01 case took three times as long as the 1.0 case for that same increment.
Bulk vel = -1.0
Bulk vel = -0.1
Bulk vel = -0.01
