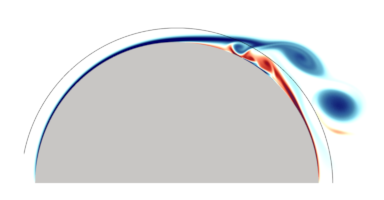
M. Stock, A. Gharakhani, A Hybrid High-Order Vorticity-Based Eulerian and Lagrangian Vortex Particle Method, The 2-D Case [PDF paper] [PDF slides], Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, August 10-12, 2021, Virtual.
My research focus is vortex particle methods for flow simulation. In the last two decades I have created a number of Eulerian, Lagrangian, and hybrid vortex methods in both two- and three-dimensions, some independent and many with Applied Scientific Research in Irvine, California, USA. In addition, I am interested in GPU and parallel programming, computational geometry, cellular automata, and high-resolution image rendering and display. See my research on ORCID, Google Scholar, and Scopus, or browse my open-source codes on github.
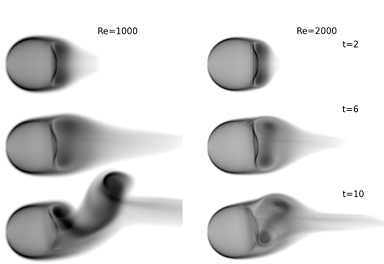
Hybrid CFD methods aim to leverage the benefits of both types of solvers, using Eulerian methods near boundaries or in regions of high gradients, and Lagrangian methods in unsteady convecting wakes. At ASR, we pioneered this combination in 2010 with a system joining NASA's OVERFLOW2 code with our OmegaFlow GPU-accelerated 3D vortex particle method. And in 2021 we were the first to hybridize a high-order Eulerian method with our open-source Lagrangian Vortex Particle Methods solver, resulting in much smaller overlap regions than any previously reported work.

M. Stock, A. Gharakhani, A Hybrid High-Order Vorticity-Based Eulerian and Lagrangian Vortex Particle Method, The 2-D Case [PDF paper] [PDF slides], Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, August 10-12, 2021, Virtual.
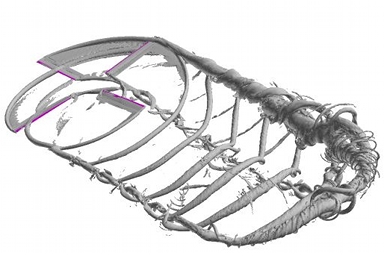
M. Stock, A. Gharakhani, and C. Stone, Modeling Rotor Wakes with a Hybrid OVERFLOW-Vortex Method on a GPU Cluster [PDF paper] [PDF slides] [Movie at YouTube], AIAA 28th AIAA Applied Aerodynamics Conference, 28 Jun-1 Jul 2010, Chicago, IL.
The "order" of a computational method is the power of the error term on the element size or time step size. First order methods, for example, have an error term that changes linearly with the element or time step size: elements are half as large means the error is half as large. "High" order methods approach the true solution (their expected error scales) with the 3rd or higher power of the element or time step size, so using elements half as large makes the error one eighth as large or better. Thus, fewer computational elements or time steps are required to achieve the desired accuracy. Often, though, the algorithms are more intricate and possibly less stable. Here is the first of several new high-order methods for vorticity-based CFD that my collaborators and I have created.
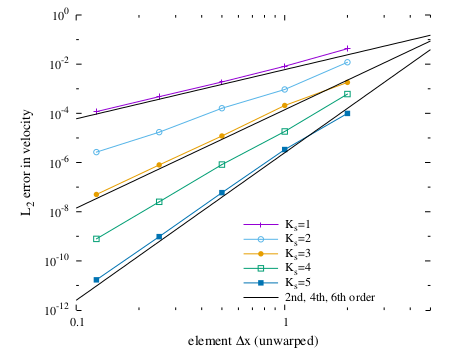
A. Gharakhani, M. Stock, A Method for Numerical Evaluation of Singular Integrals in Curved Hexahedra and with High-Order Source Functions[PDF paper], Proceedings of the ASME 2022 Fluids Engineering Division Summer Meeting, August 3-5, 2022, Toronto, Canada.
Most computational fluid dynamics (CFD) algorithms use Eulerian methods, in which flow moves through fixed, regular triangular or rectangular elements. In addition, they use velocity-pressure coordinates, which allows simulation of compressible flows, but imposes severe limitations on time step size and algorithmic stability. A cure to that is Stam's Stable Fluids method, which makes a fluid simulation stable, but at the cost of large numerical dissipation. My solution to these problems is a novel backward-timestep Semi-Lagrangian vortex method. Here are CPU and GPU versions of that method, first implemented in 2004.

Digital Ebru, a 2D real-time fluid simulator with extremely low diffusion, is written in Lua and OpenGL. Vorticity is advected using a 4th order Runge-Kutta method with 4th order M4' interpolation kernels. Velocity is computed from vorticity using a multigrid solver implemented in OpenGL compute shaders - which I believe is the first time that has been done. The code is open-source, and uses J. Susinno's OpenGL With Luajit framework.

vic2d is the original, C-based, 2D fluid simulator from 2004. Similarly, vorticity is advected using a 4th order Runge-Kutta method with 4th order M4' interpolation kernels, but velocity is computed using a multithreaded multigrid solver for the CPU. The code is open-source, and has a minimum of dependencies.
Recently, Applied Scientific Research has released an open source project for 2D flows to github. It is part of an ongoing NIH-funded project to create a new tool to improve heart valve designers' design toolbox. Relevant software and papers include the following.
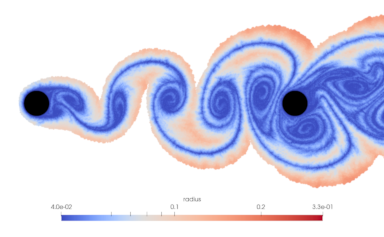
M. Stock, A. Gharakhani, Solution-Responsive Particle Size Adaptivity in Lagrangian Vortex Particle Methods [PDF] [PDF slides], Proceedings of the ASME 2021 Fluids Engineering Division Summer Meeting, August 10-12, 2021, Virtual. This is the first truly solution-adaptive Lagrangian Vortex Particle Method capable of tuning unquantized local particle sizes in order to most evenly capture a flow without excess resolution.

Omega2D is a new, real-time 2D fluid simulator with GUI written in C++. It merges a standard Lagrangian Vortex Particle Method with a panel-based Boundary Element Method to make a complete tool. The code is open-source, borrows from a number of header-only libraries, and should compile on Linux, Windows, and MacOS.

M. Stock and A. Gharakhani, Open Source Accelerated Vortex Particle Methods for Unsteady Flow Simulation [PDF paper], ASME 2020 Fluids Engineering Division Summer Meeting, Jul 12-16, 2020, Orlando, FL.
The most capable vortex methods stem from discretization of vorticity as Lagrangian vortex blobs, with the vorticity-velocity inversion calculated using a multipole-accelerated treecode, Fast Multipole Method, or Vortex-in-Cell method. Applied Scientific Research is currently conducting advanced research in vortex particle methods, including Large-Eddy Simulation, efficient parallel treecodes, and GPGPU for vortex simulation. Publications that I have been involved with at ASR follow.
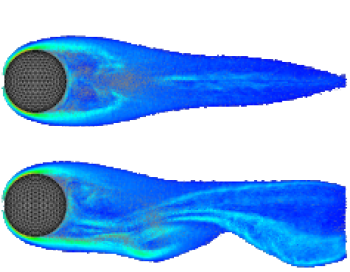
M. Stock and A. Gharakhani, A GPU-accelerated Boundary Element Method and Vortex Particle Method [PDF paper] [PDF slides], AIAA 40th Fluid Dynamics Conference and Exhibit, 28 Jun-1 Jul 2010, Chicago, IL.

M. Stock and A. Gharakhani, Toward efficient GPU-accelerated N-body simulations [PDF paper] [PDF slides], 46th AIAA Aerospace Sciences Meeting, 7-10 January 2008, Reno, NV.

A. Gharakhani and M. Stock, 3-D Vortex simulation
of flow over a circular disk at an angle of attack, 17th AIAA Computational Fluid
Dynamics Conference, 6-9 June 2005, Toronto, Canada.
A. Gharakhani, J. Sitaraman, M. Stock, A Lagrangian vortex method for simulating flow over
3-D objects, 2005 ASME Fluids Engineering Division Summer Meeting, June 19-23,
Houston, TX.
My dissertation research concerned three-dimensional vortex sheet methods for inviscid simulation. At the time, the only three-dimensional vortex sheet methods could not track flows for very long times because they were limited either by rectangular or curvature-dependent discretization methods. My donation to the field was a front-tracking vortex sheet method that used edge splitting and node merging to accomplish long-time simulation of inviscid vortex sheet flows. The research spawned a paper appearing in the Journal of Computational Physics.

M. Stock, W.J.A. Dahm, G. Tryggvason, Impact of a vortex ring on a density interface using a regularized inviscid vortex sheet method, Journal of Computational Physics, 227/21, pp. 9021-9043, Nov. 2008, 2.5 MB PDF

M. Stock, A Regularized Inviscid Vortex Sheet
Method for Three Dimensional Flows With Density Interfaces, PhD thesis,
University of Michigan, Ann Arbor, 2006, 7.0 MB PDF
In the process of conducting this research, I assembled a summary of the major aspects of vortex methods research as well as 415 literature references. It is a living document, and thus contains not only references and questions, but my throughts regarding various lines of research. I am making it available in the hopes that newcomers to the field might find it useful.
M. Stock, Summary of Vortex Methods Literature, unpublished, 2007, 1 MB PDF